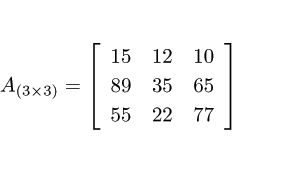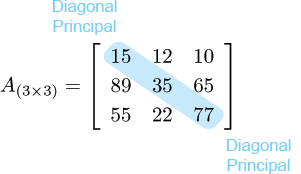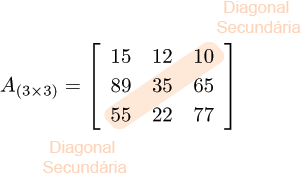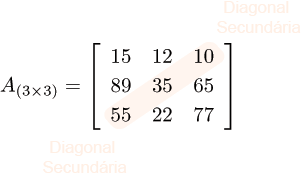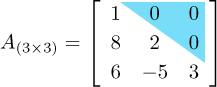Matriz Quadrada
Dizemos que A é uma matriz quadrada ou quadrática quando o número de linhas dessa matriz é igual ao seu número de colunas. Diz-se que uma matriz quadrada com m linhas e m colunas tem ordem m, simplificando a representação geral de ordem de matrizes que seria m x m, nesse caso. Uma matriz quadrada tem o seguinte aspecto geral:
A(m×n)=[a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮am1am2⋯amn]
Veja um exemplo de matriz quadrada de ordem 3:
A(3×3)=[151210893565552277]
Em uma matriz quadrada, os elementos alinhados a partir do canto superior esquerdo até o canto inferior direito constituem sua diagonal principal. Na matriz exemplo mostrada anteriormente, a diagonal principal é formada pelos elementos 15, 35 e 77. No caso geral, a diagonal principal é formada pelos elementos a11,a22,a33,…,amn, ou seja, aii, para todo i∈{1,2,3,⋯,m}. Analogamente, a diagonal secundária de uma matriz quadrada é formada pelos elementos alinhados a partir do canto inferior esquerdo até o canto superior direito. Nessa matriz exemplo, a diagonal secundária é dada pelos elementos 55, 35 e 10. No caso geral, a diagonal secundária é dada pelos elementos a1m,a2(m−1),⋯,am1, ou seja, ai(m−i+1), para todo i∈{1,2,3,⋯,n}.
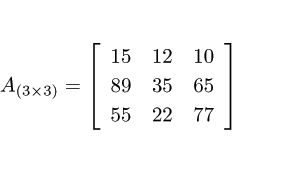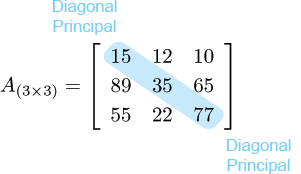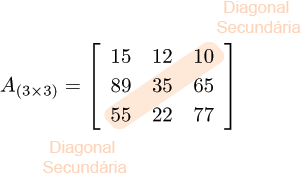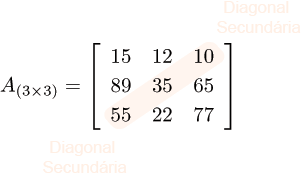
Matriz Triangular
Uma matriz triangular inferior é uma matriz quadrada em que todos os elementos acima de sua diagonal principal são nulos. Em outras palavras, dizemos que uma matriz quadrada é uma matriz triangular inferior quando aij=0 sempre que j>i. A seguir, apresentamos um exemplo de matriz triangular inferior de ordem 3.
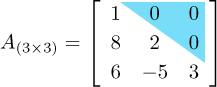
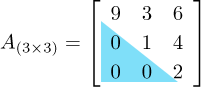
Uma matriz triangular superior é uma matriz quadrada em que todos os elementos abaixo de sua diagonal principal são nulos, isto é, aij=0 sempre que j<i. Segue-se um exemplo de matriz triangular superior.
Exemplo 1
Considere uma propaganda de uma companhia de televisão a cabo com 3 tipos de pacote: o pacote 1, que custa R$30/mês, o pacote 2, que custa R$50/mês e o pacote 3, que custa R$60/mês.
O conteúdo de cada pacote é um subconjunto próprio do conteúdo dos pacotes superiores (conteúdo 1⊂ conteúdo 2 ⊂ conteúdo 3). A matriz triangular superior a seguir poderia ser usada por um programa computacional que diria quanto o cliente deve pagar a mais, caso queira mudar de um dado pacote para um pacote superior.
Diferença de tarifas para pacote superior=[020300010000]
Nessa matriz, cada linha corresponde ao pacote atual do cliente e cada coluna corresponde ao pacote desejado. Note que essa matriz é triangular superior, pois a21=a31=aa32=0. Se um programa precisar calcular o que o cliente deve pagar a mais para migrar do pacote 1 para o 3, por exemplo, ele consultará a posição a13, obtendo o valor 30. Como só estamos nos preocupando com a migração para pacotes superiores, podemos colocar zeros nas casas correspondentes a migrações para pacotes inferiores, pois essas casas não serão acessadas. Se fôssemos modelar o problema completo com migrações para pacotes superiores e inferiores, essa matriz não seria mais triangular (mas bem que as companhias de TV a cabo gostariam de nos fazer migrar para pacotes inferiores pagando a mesma coisa, não é?).
Se liga!
Nesse exemplo, a diagonal também é composta de zeros. Isso não é necessário para que uma matriz seja triangular superior, mas não impede que ela seja! O que você precisa verificar é se os elementos abaixo da diagonal principal são nulos para que a matriz seja triangular superior. Analogamente, verificar se os elementos acima da diagonal principal são nulos para que a matriz seja triangular inferior.