Maneira 2

Maneira 2: Nessa resolução utilizamos a técnica de regra de três composta para resolver o problema mais rapidamente.

• Mostrar Solução arrow_drop_down

  Você deve começar a resolver o problema montando a tabela de grandezas, colocando em cada coluna os valores de cada grandeza e, em cada linha, os valores das grandezas diferentes que têm relação entre si:

  Número de funcionários	Carga horária	Quantidade de produtos
  20	6	450
  x	8	900

  Em seguida, você deve definir se a carga horária e a quantidade de produtos são diretamente ou inversamente proporcionais ao número de funcionários, a grandeza da incógnita x. Por convenção, colocaremos uma seta para baixo em número de funcionários. Se aumentarmos o número de funcionários, mantendo a quantidade de produtos, precisaremos de uma carga horária menor (então, colocaremos uma seta contrária ao número de funcionários). Por outro lado, se aumentarmos o número de funcionários, mantendo a carga horária, teremos uma quantidade de produtos maior (então, colocaremos uma seta na mesma direção do número de funcionários). Portanto, a carga horária e a quantidade de produtos são inversamente e diretamente proporcionais ao número de funcionários, respectivamente. Os sentidos das setas na tabela seguinte indicam a proporcionalidade entre as grandezas:

  

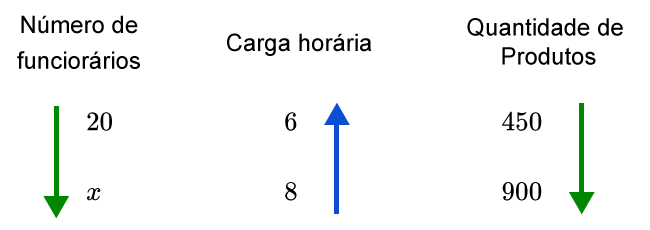
  Finalmente, você montará a proporção correspondente, lembrando de inverter as razões correspondentes às grandezas inversamente proporcionais ao número de funcionários:

  $$\frac{20}{x} = \frac{8}{6} \cdot \frac{450}{900} \Rightarrow \frac{20}{x} = \frac{8 \cdot 450}{6 \cdot 900} \Rightarrow x = \frac{20 \cdot 6 \cdot 900}{8 \cdot 450} = 30$$

  Logo, a fábrica precisará de 30 funcionários para atingir a produção desejada em 8 horas diárias de trabalho.