Saída - Como os computadores nos apresentam resultados?

Ok, ok... os computadores percebem tudo e calculam tudo através de 0's e 1's, mas se eles nos apresentassem os resultados dos cálculos com 0's e 1's seria de uso inviável para muitas pessoas, simplesmente por nunca terem estudado o sistema de numeração binário. Você pode até se perguntar porque então não utilizar logo o sistema binário nas escolas desde cedo. Para ver algumas vantagens históricas para se usar uma determinada base, você pode assistir o já recomendado vídeo do programa português Isto É Matemática, o episódio É Aquela Base. Então, vejamos exemplos de como um computador transforma e consegue nos apresentar resultados de uma forma útil, ou seja, como um monte de 0's e 1's se transformam em imagens de caracteres ou imagens que conseguimos, ler.

Matrizes na representação de imagens digitais

As telas de TV, computadores e celulares são formadas por uma grade de vários pontos pequeninos chamados de pixels. Um pixel é o menor elemento de uma imagem (Picture Element), vindo daí o seu nome. Essa grade de pontos também pode ser chamada de matriz de pixels, e quanto maior o número de pixels em uma determinada área da tela, maior a sua resolução e melhores serão as imagens. As imagens, por sua vez, também são grandes matrizes compostas de vários pontos. A junção desses pontos compõe uma foto digital como a conhecemos. Ao ampliarmos várias vezes uma imagem, podemos notar que ela vai ficando quadriculada ou como dizemos, com aspecto pixelado. Assim como nas telas, quanto maior o número de pixels uma imagem puder representar, melhor será a sua qualidade. Vemos essa denominação nas câmeras de foto quando dizem, por exemplo, que certa câmera é de 14 Megapixels - então uma foto tirada com essa câmera poderá representar até 14 milhões de pixels. A seguir, vemos um exemplo simples da representação de como uma figura de uma letra (A) pode ser representada através de uma matriz no computador.

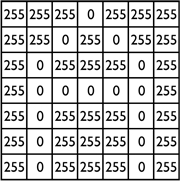
Nessa imagem, cada posição da matriz corresponde à representação de um pixel. Para uma figura em escala de cinza, o computador entende que existem 255 níveis de branco, sendo 255 o branco total e 0 sendo o preto total. Então, o computador pinta na tela cada posição da matriz com sua devida cor e teremos:

Cada campo dessa matriz de representação possui um valor, e é o tamanho da matriz que vai nos dizer a resolução dessa imagem. Assim, cada vez que aumentarmos o tamanho da matriz (representando mais pixels) para representar o mesmo A, teremos uma imagem de melhor qualidade.

É basicamente a mesma ideia do ponto-cruz que sua mãe ou avó fazia, todas as imagens são representadas dessa forma no seu computador. Faça um teste: abra uma figura qualquer no Paint e aumente gradualmente o zoom de visualização, você vai ver que essa matriz vai ficar cada vez mais visível ao ponto que as imagens vão ficando “pixeladas”.

Porém, como queremos ver figuras coloridas, o computador reconhece três cores principais: vermelho, verde e azul (o famoso RGB). Assim, cada pixel pode ser representado por 3 números: um tom de vermelho, um tom de azul e um tom de verde - todas as cores que vemos no nosso computador são uma mistura dessas 3 cores. Uma figura colorida então é formada por uma matriz de 3 dimensões, ou 3 matrizes normais como conhecemos, sendo cada matriz responsável pela representação de uma camada de cor. Vejamos um exemplo.

Além da representação, podemos usar matrizes especiais que servem como filtros para adicionarmos efeitos às imagens (como os efeitos que fazemos no Photoshop, por exemplo), ou analisarmos aspectos importantes em uma imagem (como detecção de bordas e objetos, aspectos essenciais para sistemas de mapas e navegação robótica).

Ao realizarmos um tipo de multiplicação da matriz de representação de imagem com uma dessas matrizes especiais, obtemos efeitos como: